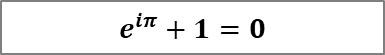​最美数学公式 欧拉公式 和 泰勒展开式 - 微积分应用

最美数学公式 欧拉公式 和 泰勒展开式 - 微积分应用

我们在另一篇文章中同样介绍过，被称作最美数学公式的欧拉公式：

欧拉公式

本文用泰勒展开式（麦克劳林公式）来加以证明。

简单介绍一下泰勒展开式，它使用幂函数的线性组合来逼近/近似函数。

泰勒展开式的一般形式如下：

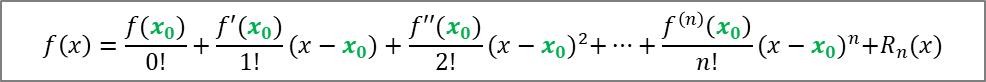
泰勒展开式

泰勒展开式在x=0处的展开式，被称作麦克劳林公式，如下：

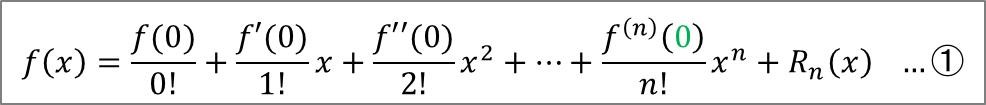
麦克劳林公式

*关于泰勒展开式或者麦克劳林公式，本文不做特别说明，后期有机会专门写一篇文章来介绍。

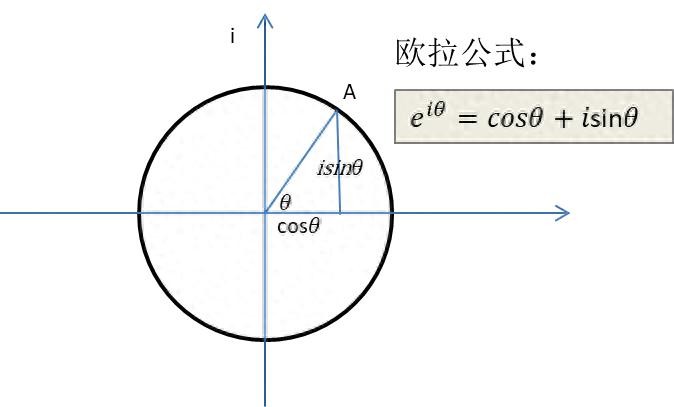
欧拉公式：

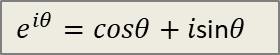
等式左右联系了3个函数，分别对其计算1-5阶导数，结果如下：

对3个函数求导数

分别代入麦克劳林公式，

正弦函数 sinx 的麦克劳林公式：

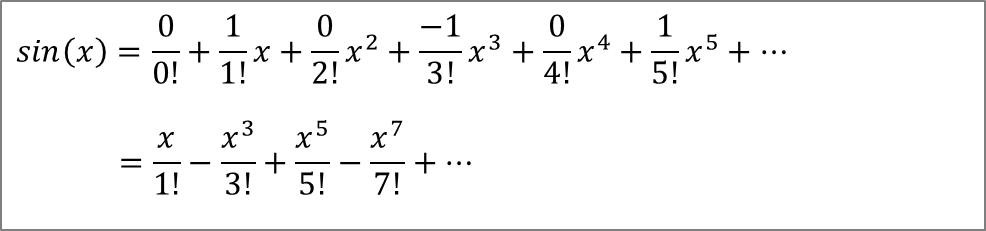
正弦函数的麦克劳林公式

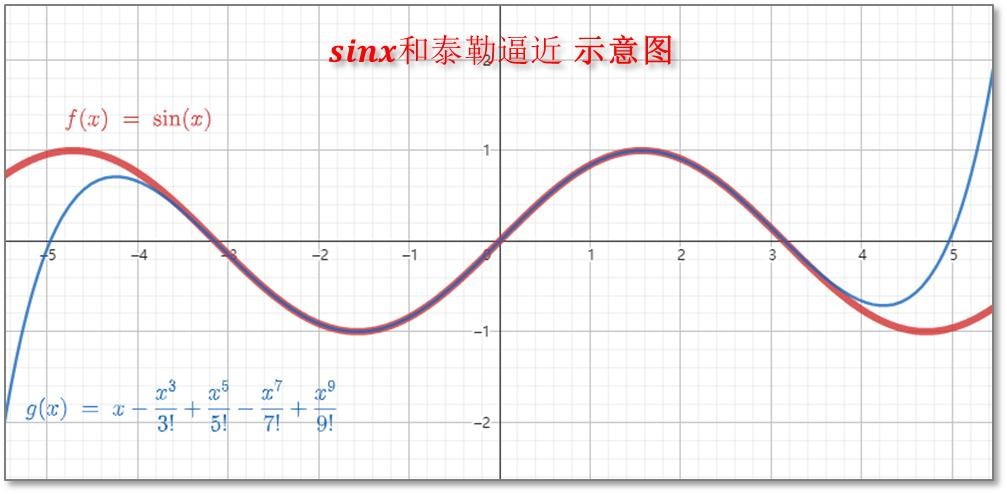
红色为 sinx 的函数图，蓝色为泰勒逼近（逼近到x的9次方），

可以看出，x在[-3, 3]区间内，红色和蓝色几乎重合，也就是说，在此区间内，计算到

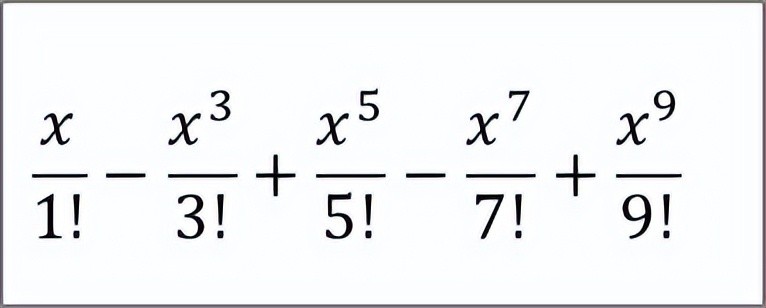
就可以得到非常精确的正弦函数值。

如果需要计算x在[-3, 3]之外的区间，多逼近几次就可以得到所需要的精度。

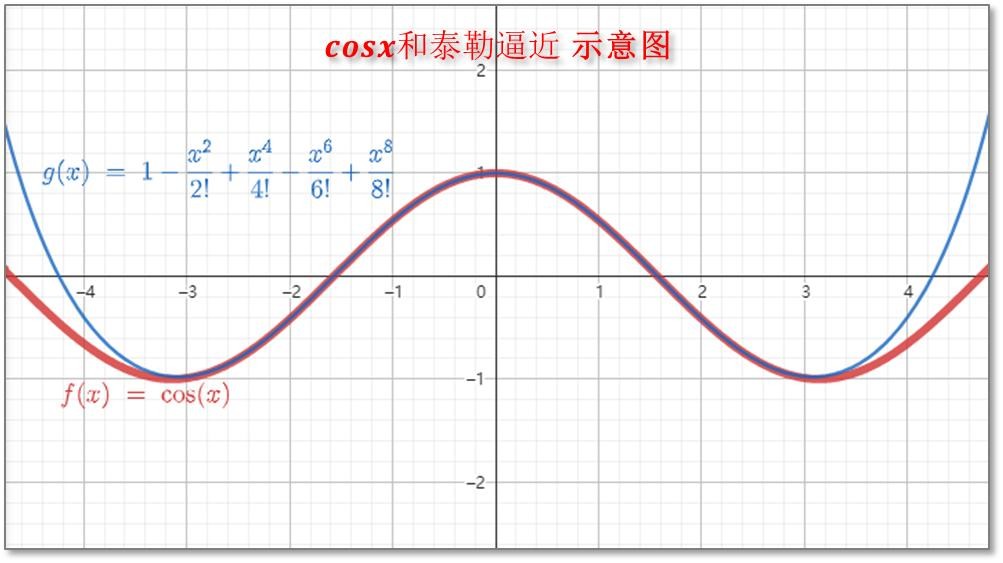
余弦函数 cosx 的麦克劳林公式：

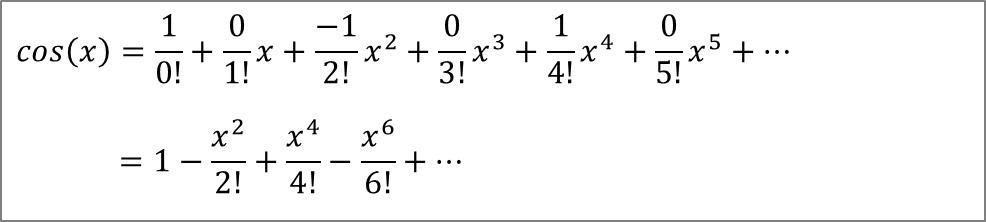
余弦函数的麦克劳林公式

e的指数函数 的麦克劳林公式：

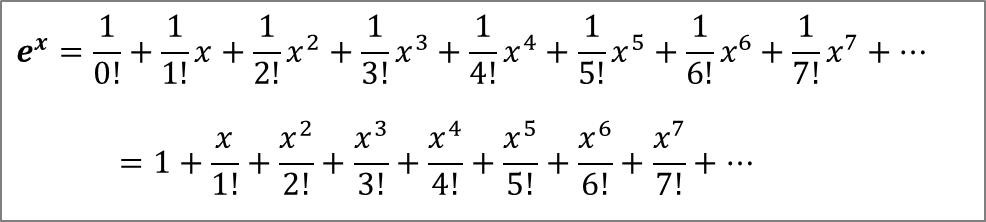
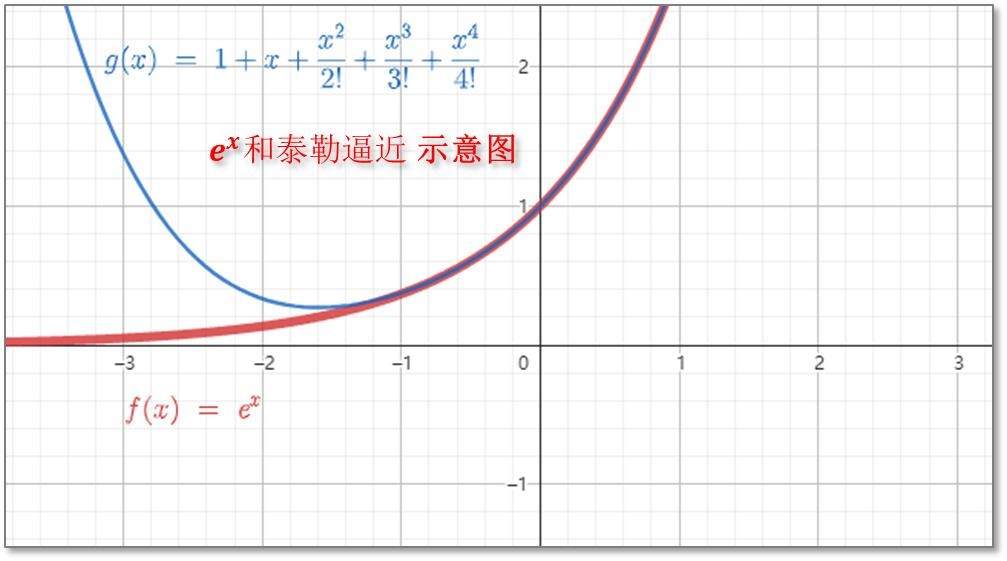
下面利用上面3个函数的麦克劳林公式，来证明欧拉公式：

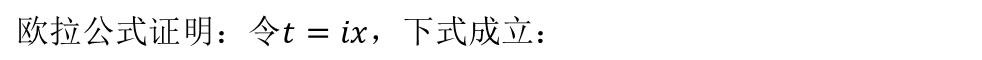
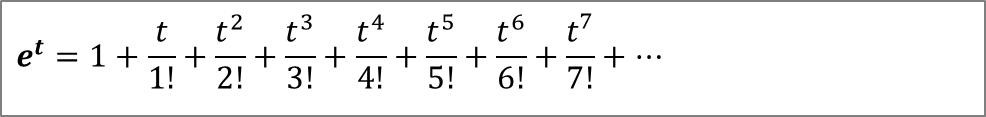
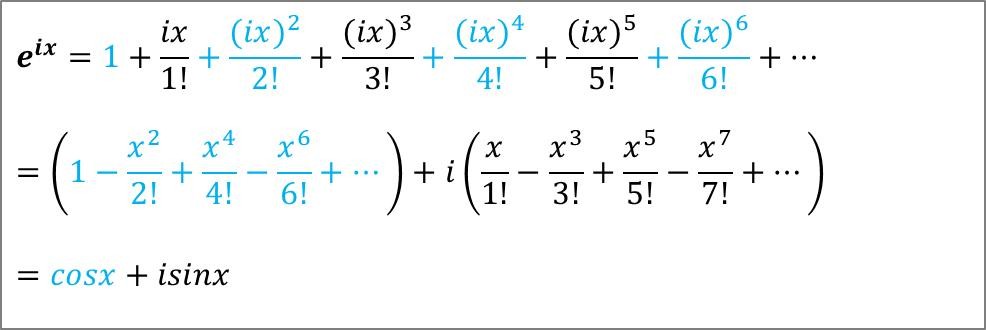
得到如下欧拉公式：

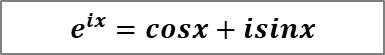
特别，当x=π时，有：